Question 1

1. 1. 25 * 3   no
   2. 5 ^ 2 * 3   yes
   3. (5 ^ 2) * 3   no
   4. 5 * 2 * 3   yes

2. There are two kinds of ambiguity:
   1. Associativity of ^
   2. Precedence between * and ^
   An example of the first is:

   
             Exp            Exp
             /|\            /|\
            / | \          / | \
          Exp ^ Exp      Exp ^ Exp
          /|\    |        |    /|\
         / | \   |        |   / | \
       Exp ^ Exp Num    Num Exp ^ Exp
        |     |  |        |  |     |
        |     |  |        |  |     |
       Num   Num 4        2 Num   Num
        |     |              |     |
        |     |              |     |
        2     3              3     4
   
   

   An example of the second is:

   
             Exp            Exp
             /|\            /|\
            / | \          / | \
          Exp ^ Exp      Num * Exp
          /|\    |        |    /|\
         / | \   |        |   / | \
       Num * Exp Num      2 Exp ^ Exp
        |     |  |           |     |
        |     |  |           |     |
        2    Num 4          Num   Num
              |              |     |
              |              |     |
              3              3     4
   
   

3. An equivalent non-ambiguous grammar where ^ has precedence over * is the following:

      Exp ::= Exp * A | B
        A ::= C ^ A | Num 
        B ::= C ^ B | C
        C ::= Num | (Exp)
      Num ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
   

   An equivalent non-ambiguous grammar where * has precedence over ^ is the following:

      Exp ::= A ^ Exp | A
        A ::= Num * A | Num | (Exp)
      Num ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
   

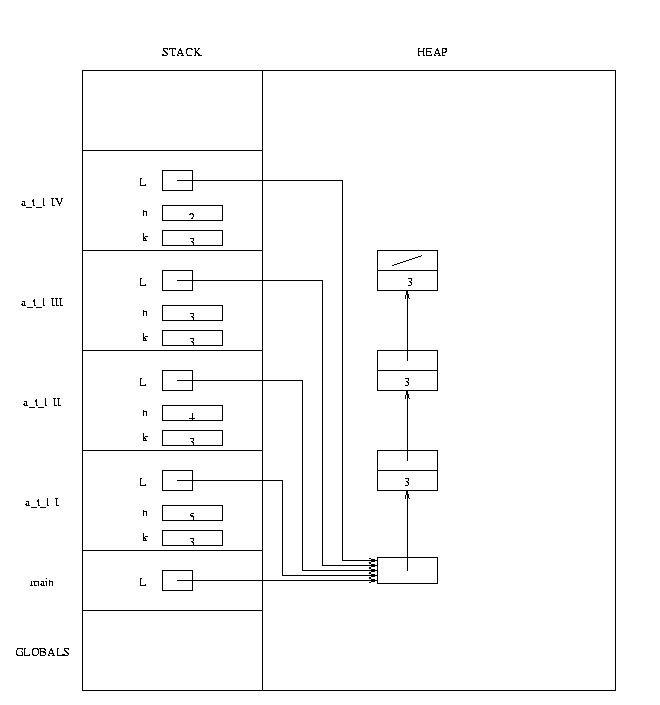
Question 2 (Memory management)

Question 3 (Concurrency in Java)

  class Account {

      private int balance;

      public Buffer(int initialDeposit) { balance = initialDeposit; }

      public synchronized int getBalance() {
         return balance;
      }

      public synchronized void deposit(int amount) { 
         if (amount < 0)
            error(1) % the amount to deposit should be non negative
         else {
            balance = balance + amount;
            notifyAll();
         }
      }

      public synchronized void withdraw(int amount) { //we omit the treatment of interruptedExeption
         if (amount < 0)
            error(1) % the amount to withdrow should be non negative
         else {
            while (balance < amount) wait();
            balance = balance - amount;
         }
      }
   }

   class AccountHolder extends Thread {
       Account a;
       ...
       public void run() {
               ...
               a.deposit(x);
               ...
               a.withdraw(y); // no need to test that the balance is greater than or equal to the amount to withdraw
               ...
       }
   }

Question 4 (ML)

   fun max(x,y) = if x > y then x else y;

   fun heights(leaf x) = leaf 1
     | heights(node(t1,x,t2)) = let val (h1,u1) = heights t1
                                and val (h2,t2) = heights t2
                                 in node(u1, max(h1,h2)+1, u2)
                                end;

   fun root (leaf x) = x
     | root (node(t1,x,t2)) = x;
 
   fun heights(leaf x) = leaf 1
     | heights(node(t1,x,t2)) = let val u1 = heights t1
                                and val u2 = heights t2
                                 in node(u1, max(root u1, root u2) + 1, u2)
                                end;

Question 5 (Prolog)

   divisor_and_rest(M,N,X,Y) :- nat(X,N), nat(Y,N), N is M * X + Y.

   nat(M,M) :- M >= 0.
   nat(X,M) :- M > 0, N is M - 1, nat(X,N).

Question 6 (Prolog)

   conc([],[]).
   conc([X|L],K) :- conc(L,M), append(X,M,K).