


On considère un langage PASCAL très simplifié, avec des variables globales entières, des expressions entières et booléennes, et les instructions d’affectation, de test et de boucle while :
|
count := 0; sum := 1; while sum <= n do count := count + 1; sum := sum + 2 * count + 1 doneAffirmation : à la fin de l’exécution de ce programme, count est la racine carré de n, arrondie à l’entier inférieur.
Un état d’un programme est une table d’association E qui à chaque variable x du programme associe sa valeur courante E(x). La valeur d’une expression bien typée e dans un état E est définie par
|
La sémantique opérationnelle de ce langage est définie par les règles de transition (sur toute instruction bien typée) :
|
Un triplet de Hoare est un triplet noté {P} i {Q} où P et Q sont des assertions logiques et i une instruction. Ces assertions logiques sont des formules du premier ordre, avec comme formules atomiques les expressions de notre langage. Remarque importante : il y a ainsi identification entre les variables du programme et les variables de la logique.
On dit qu’un triplet de Hoare {P} i {Q} est valide si pour tous états E1 et E2 tels que E1→i E2 et P est vraie dans E1, Q est vraie dans E2.
Exemples de triplets valides : {x=1} x:=x+2 {x=3}, {x=y} x:=x+y {x=2y}.
| {n ≥ 0} ISQRT {count*count ≤ n ∧ n < (count+1)*(count+1)} |
Logique de Hoare : ensemble de règles de déduction sur les triplets :
|
Preuve : pas de difficulté (cf chapitre 2).
Difficulté : prouver un triplet à partir de ces règles demande de « deviner » les bonnes annotations intermédiaires, par exemple pour la séquence, mais aussi pour la règle d’affaiblissement. Ainsi, on ne peut pas prouver le programme de la racine carrée sans réfléchir : il faut en particulier trouver un invariant de boucle adéquat. L’équivalent, du point de vue théorique, de cette difficulté est : a-t-on complétude de la logique de Hoare, c.-à-d. peut-on prouver tous les triplets valides ?
Pour i et Q fixés, l’ensemble des P tels que {P} i {Q} est valide, s’il est non vide, possède-t-il un élément minimal P0 au sens où pour tout P tels que {P} i {Q} est valide, P implique P0.
Calcul de WP :
|
Preuve : le relativement exprime ici une hypothèse qui est que la logique dans laquelle on exprime les annotations est suffisamment expressive, en particulier pour exprimer les invariants de boucle nécessaires à l’aide de point-fixe [Cou90].
De nombreux travaux ont fait suite à la logique de Hoare originale [Cou90], pour étendre le formalisme et résoudre des difficultés, par exemple :
break, continue, les exceptions.let isqrt = fun (n : int) -> { n >= 0 } (* pré-condition *) begin let count = ref 0 in let sum = ref 1 in begin while !sum <= n do { invariant count >= 0 and n >= count*count and sum = (count+1)*(count+1) variant n - sum } (* invariant et variant de boucle *) count := !count + 1; sum := !sum + 2 * !count + 1 done; !count end end { result >= 0 and result * result <= n and n < ( result+1)*( result+1) } (* post-condition *)
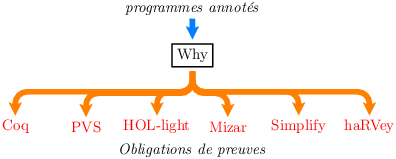
Objectif général : établir la validité d’un triplet de Hoare, non pas avec les règles de déduction précédente, mais avec une technique fondée sur le calcul des constructions inductives. Cet objectif a été développé par Jean-Christophe Filliâtre [Fil03a] et implantée dans un outil logiciel appelée Why [Fil03b]. Les programmes traités par Why ne sont pas en PASCAL, ni en C ou autre langage de programmation existant, mais dans une syntaxe spécifique, qui a été conçue pour la preuve de ces programmes.
En Why, toutes les difficultés mentionnées ci-dessus sont traitées, exceptés la possibilité d’avoir des structures de données complexes et les entiers bornés. Dans la section suivante, nous verrons à la fois comment traiter les structures de données complexes, et comment faire des preuves sur des programmes écrits dans des langages de programmation impératifs standards : Java ou C en l’occurrence.
La figure 8.1 donne de nouveau le programme qui calcule la racine carrée, écrit cette fois sous forme d’une fonction Why. On remarque que :
Le travail de l’outil Why consiste à produire, à partir d’un programme annoté, des obligations de preuves dont la validité assure la correction du programme. Avec Why, ces obligations de preuves sont des formules en logique du premier ordre, exprimable dans la syntaxe de différents démonstrateurs existants, aussi bien des démonstrateurs interactifs comme Coq, PVS, HOL-light ou Mizar, que des démonstrateurs automatiques comme Simplify ou haRVey.
Néanmoins, la sortie pour Coq possède une particularité supplémentaire : la validation, qui est un programme fonctionnel Coq équivalent au programme de départ. Il s’agit là de l’idée directrice de l’approche Why : un programme impératif peut être traduit en un programme fonctionnel par ajout de paramètre. Sur l’exemple de ISQRT, on écrirait quelque chose comme
isqrt(n) = isqrt2(n,0,1) isqrt2(n,count,sum) = if sum<=n then isqrt2(n,count+1,sum + 2 * (count+1)+1) else count
On est ramené alors à la preuve d’un programme fonctionnel. Il s’agit là d’une instance de l’approche par plongement superficiel (shallow embedding en anglais) opposé à plongement profond (deep embedding), tel qu’expliqué dans le chapitre 2.
C’est un langage fonctionnel auquel sont rajoutés quelques traits impératifs. Les types de base sont : int, bool, float et unit (habité par la constante void). Comme d’habitude avec les langages fonctionnels, il n’y a pas de distinction syntaxiques entre expressions et instructions : les instructions sont les expressions de type unit.
Le noyau fonctionnel est constitué des expressions suivantes :
Les traits impératifs sont introduits par
Remarque : pour simplifier on ne traite pas les définitions récursives ici, ni la levée et le rattrapage d’exception. Le langage complet est décrit dans le manuel utilisateur.
En Why, toute expression e peut être annotée, avec la notation des triplets de Hoare { pre } e { post }. Les boucles while doivent être annotée par
| while e do { invariant inv variant var } e done |
pour spécifier un invariant de boucle, ainsi qu’un variant, une expression censée décroitre à chaque itération de la boucle, assurant ainsi la terminaison. Les annotations pre, post et inv sont des formules de logique du premier ordre, leur variables sont les variables du programme. De plus, dans les post on peut utiliser le mot-clé result pour référer à la valeur résultat de l’expression, et v@ pour désigner la valeur de v avant l’exécution de l’expression.
Comme un langage de programmation classique, le langage Why possède des règles de typage, et un programme doit être correctement typé pour que la génération des obligations de preuves puissent se faire. Comme ce langage est proche de Caml, le type en est assez proche aussi, mais on lui ajoute une spécificité qui est le typage des effets, qui consiste à préciser quelles sont les références qui sont lues et celles qui sont écrites.
Voici un exemple de programme très simple, qui va nous servir pour illustrer les mécanismes de Why :
parameter montant : int ref let crediter = fun (s:int) -> { s >= 0 } montant := !montant + s { montant = s + montant@ }
En tant que programme « Caml », on sait très bien inférer que
crediter a le type int -> unit. Ce qu’on va faire en
plus c’est de calculer ses effets, pour déterminer dans cet exemple
que la référence montant est à la fois lue et écrite.
Un type avec effet est un triplet (type, variables lues, variables écrites). Voici un extrait des règles de typage de Why (cf [Fil03a] pour le reste).
|
La règle de typage de l’application ci-dessus interdit d’appliquer une fonction à une référence. Une règle spéciale existe dans ce cas :
|
Il est fondamental de remarquer que cette règle interdit les alias, c.-à-d. de référencer la même chose avec deux noms différents. C’est une condition essentielle pour garantir la correction de la méthode Why. Voici un exemple typique :
let incr2 = fun (x:int ref) (y:int ref) ->
{ true } begin x := !x + 1; y := !y + 1 end { x = x@ + 1 and y = y@ + 1 }
parameter t : int ref
let test = { true } (incr2 t t) { t = t@ + 1 }
Why signale une erreur de typage sur l’application (incr2 t t). Si c’était accepté, alors au vu de la
post-condition de incr2, la post-condition t = t@ + 1
serait prouvable, or elle est fausse, c’est t=t@ + 2 qui est
vrai.
| montant:int ref ⊢ crediter : (int→ (unit,{montant},{montant}),∅,∅)) |
On peut utiliser cette approche de typage avec effets pour définir des programmes Why de façon modulaire : un programme peut très faire appel à une autre fonction dont le code n’est pas donné, cette fonction doit seulement être spécifiée par son type avec effets, ainsi qu’avec un pré et une post-condition. Par exemple on peut écrire :
parameter montant : int ref parameter crediter : s:int -> { s >= 0 } unit reads montant writes montant { montant = s + montant@ } let test = fun (tt:unit) -> { true } begin (crediter 50); (crediter 80) end { montant = montant@ + 130 }
Avec l’inférence de type avec effets, on est capable d’associer à chaque sous-expression d’un programme un type avec effets. L’étape suivante consiste à leur associer aussi une pré et une post-condition : de deux choses l’une : soit l’expression considérée est déjà annotée (une boucle while, un identificateur de fonction, ou une expression explicitement annotée par l’utilisateur), soit on lui détermine une annotation par calcul de plus faible pré-condition, d’une manière très similaire à celui de la logique de Hoare classique, mais adaptée au langage Why.
Voici un extrait des formules de calcul de WP, les règles complètes sont dans le manuel de Why [Fil02] et dans [Fil99] .
|
La règle pour l’application est l’une des plus complexe :
|
si f a le type avec effets annoté x1:t1⋯ xn:tn → {Pf}
(t,R,W) {Qf}, et les expressions e1,…,en sont pures,
c.-à-d. ne modifient aucune variable. Cette dernière condition fait
qu’il peut arriver que l’outil Why peut parfois ne pas parvenir à
générer les obligations de preuves, auquel cas il faut simplifier
l’application concernée en introduisant des let…in…
crediter.
Il s’agit maintenant du cœur même de la méthode Why. Nous en donnons ici un aperçu, les détails étant dans[Fil99, Fil03a].
Le but est d’engendrer un programme fonctionnel Coq équivalent au programme Why complètement annoté. Ce programme comportera des « trous » pour les preuves des annotations logiques : les obligations de preuve. Celle-ci peuvent naturellement être prouvées dans Coq, pour obtenir alors un programme fonctionnel Coq certifié, équivalent au programme de départ, que l’on appelle la validation Why.
Tout type avec effets annoté T={P} (t,vec(r),vec(w)) {Q} est interprété en un type Coq T :
| ∀ vec(x),P(vec(x)) → ∃ vec(y),∃ r, Q(vec(x),vec(y),r) |
La notation P(vec(x)) désigne la formule P où les occurrences des
variables lues vec(r) sont substituées par les vec(x), et la
notation Q(vec(x),vec(y),r) désigne la formule Q où, pour chaque
variable v de vec(w), les occurrences de v sont remplacées par
le y correspondant, les v@ par le x correspondant, pour chaque
variable v de vec(r) qui n’est pas dans vec(w), chaque
occurrence de v est remplacée par le x correspondant, et enfin
result est remplacé par r. Il s’agit là d’exprimer le fait
que les x désignent les anciennes valeurs des variables modifiables,
alors que les y désignent les nouvelles valeurs.
En pratique, le ∃ est utilisé est celui dans Set, noté avec
des accolades. Par exemple, le type avec effet de crediter :
| s:int → {s >= 0} (unit,{montant},{montant}) { montant = s+montant@}),∅,∅) |
est interprété par le type Coq
forall (s: Z), forall (montant: Z), forall (H: s >= 0),
{ montant0: Z, result: unit | montant0 = s + montant }
Notons également que les types de base int, bool et
float sont interprétés par leurs représentations mathématiques
Coq (Z, bool et R)
et donc en particulier les entiers ne sont pas bornés.
On donne maintenant des règles de traduction d’une expression e de type avec effets T={P} (t,{r1,…,rk},{w1,…,wl}) {Q} dans un environnement Γ, en un terme Coq à trous e de type T dans l’environnement Γ obtenu en enlevant toutes les variables de type ref.
| = λ vec(x0),λ p:P(vec(x0)),(∅,x,?1) |
| = λ vec(x0),λ p:P(vec(x0)).(∅,x0,i,?1) |
| = λ vec(x0),λ p:P(vec(x0)), let (vec(x1),v,q1)=( |
| vec(x0) ?1) in (vec(x1)⊕{x ← v},tt,?2) |
| = λvec(x0),λ p:P(vec(x0)), (∅,λ x. |
| ,?1) |
| {P2}(x:t1 → {P′} (t,R′,W′){Q′},R2,W2){Q2} |
| e=λvec(x0),λ p:P(vec(x)), | let (vec(x1),a,q1) = (e1 vec(x0) ?1) in |
| let (vec(x2),f,q2) = (e2 (vec(x0)⊕vec(x1)) ?2) in | |
| let (vec(x3),v,q′) = (f a (vec(x0)⊕vec(x1)⊕vec(x2)) ?3) in | |
| (vec(x1)⊕vec(x2)⊕vec(x3),v,?4) |
| e=λvec(x0),λ p:P(vec(x0)), | let (vec(x1),f,q2) = (e2 vec(x0) ?1) in |
| let (vec(x2),v,q′) = (f r (vec(x0)⊕vec(x1)) ?2 in | |
| (vec(x1)⊕vec(x2),v,?3) |
Remarques : les interprétations de l’application évaluent les arguments de
l’application de droite à gauche. L’interprétation des boucles
while [Fil99, Fil03a] utilise
well_founded_induction tel qu’expliqué au chapitre 7.
crediter est
Definition crediter :=
(fun (s: Z) (montant: Z) (Pre: s >= 0) =>
let (result1, Post) :=
exist (fun (result: Z) => result = (s + montant))
(montant + s) (PO1 s montant Pre)
(* : { result: Z | result = s + montant } *)
in
exist_2 (fun (montant1: Z) (result0: unit) => montant1 = s + montant)
result1 tt Post)
(* : { result1: Z, result2:unit | result1 = s + montant } *)
où
PO1 (s:Z) (montant:Z) (Pre:s>=0) : montant + s = s + montant
Pour la preuve de cette proposition, il faut définir formellement la sémantique de Why [Fil99, Fil03a].
Why ne gère pas explicitement de structures de données complexes. Néanmoins, il a une approche modulaire, dans le sens où de même qu’il accepte des programmes en paramètre avec uniquement leurs spécifications, il accepte des types abstraits, et des prédicats et fonctions logiques abstraites sur ces types.
Il s’agit d’un exemple célèbre : un programme de tri linéaire quand il n’y a que trois valeurs (comme les couleurs du drapeau hollandais !) dû à Dijkstra [Dij76].
On introduit un type abstrait Why avec des axiomes :
parameter BLUE, WHITE, RED : color logic iscolor : color -> prop axiom color_elim : forall c:color. iscolor(c) -> c=BLUE or c=WHITE or c=RED
puis un premier programme Why uniquement spécifié, pour le test d’égalité des couleurs :
parameter eq_color : c1:color -> c2:color ->
{ } bool { if result then c1=c2 else c1<>c2 }
On introduit ensuite une axiomatisation des tableaux : on les représente en logique comme des tableaux « fonctionnels », c.-à-c. où la mise à jour d’une case de tableau retourne un nouveau tableau :
logic acc : colorarray, int -> color (* acc(t,i) represente t[i] *)
logic length : colorarray -> int (* longueur d'un tableau *)
logic update : colorarray, int, color -> colorarray (* mise à jour t[i] := c *)
axiom length_pos: forall t:colorarray. 0 <= length(t)
axiom length_up:
forall t:colorarray.
forall i:int. forall v:color.
length(update(t,i,v)) = length (t)
axiom acc_up_eq :
forall t:colorarray.
forall i:int. forall v:color.
acc(update(t,i,v),i) = v
axiom acc_up_neq :
forall t:colorarray.
forall i:int. forall j:int. forall v:color.
i <> j -> acc(update(t,i,v),j) = acc(t,j)
et on a les programme WHY suivant sur les tableaux :
parameter length_ : t:colorarray -> { } int { result = length(t) }
parameter acc_ : t:colorarray -> i:int ->
{ 0 <= i < length(t) }
color
{ result=acc(t,i) }
parameter update_ : t:colorarray ref -> i:int -> v:color ->
{ 0 <= i < length(t) }
unit reads t writes t
{ t = update(t@,i,v) }
noter les préconditions sur les bornes des tableaux utilisés.
On peut maintenant commencer par un petit programme qui echange deux éléments d’un tableau :
let swap = fun (t : colorarray ref) (i:int) (j:int) ->
{ 0 <= i < length(t) and 0 <= j < length(t) }
let ti = (acc_ !t i) in
let tj = (acc_ !t j) in
begin
(update_ t i tj);
(update_ t j ti)
end
{ length(t) = length(t@) and
acc(t,i) = acc(t@,j) and
acc(t,j) = acc(t@,i) and
forall k:int. i <> k and j <> k -> acc(t,k) = acc(t@,k) }
Pour écrire le programme de tri de Dijkstra, on introduit un predicat
monochrome :
logic monochrome : colorarray, int, int, color -> prop
axiom mon1 :
forall t:colorarray.
forall i:int. forall j:int. forall c:color.
monochrome(t,i,j,c) -> (forall k:int. i <= k < j -> acc(t,k)=c)
axiom mon2 :
forall t:colorarray.
forall i:int. forall j:int. forall c:color.
(forall k:int. i <= k < j -> acc(t,k)=c) -> monochrome(t,i,j,c)
et le programme principal est alors
let flag = fun (t : colorarray ref) ->
{ forall k:int. 0 <= k < length(t) -> iscolor(acc(t,k)) }
begin
let b = ref 0 in
let i = ref 0 in
let r = ref (length_ !t) in
while !i < !r do
{ invariant
(forall k:int. 0 <= k < length(t) -> iscolor(acc(t,k)))
and 0 <= b and b <= i and i <= r and r <= length(t)
and monochrome(t, 0, b, BLUE)
and monochrome(t, b, i, WHITE)
and monochrome(t, r, length(t), RED)
variant r - i }
let c = (acc_ !t !i) in
if (eq_color c BLUE)
then
begin (swap t !b !i); b := !b + 1; i := !i + 1 end
else
if (eq_color c WHITE)
then i := !i + 1
else
begin r := !r - 1; (swap t !r !i) end
done
end
{ exists r:int. exists b:int.
monochrome(t, 0, b, BLUE)
and monochrome(t, b, r, WHITE)
and monochrome(t, r, length(t), RED) }
Notons que les onze obligations de preuves engendrées pour ces deux
programmes (swap et flag) sont prouvées entièrement
automatiquement par Simplify.
L’approche ci-dessus pour les tableaux simples peut être étendue à toute structure de données complexes, ce qui permet de traiter des « vrais » langages comme Java ou C : pour ceux-ci, la structure de la mémoire est modélisée avec les opérations logiques abstraites et des axiomes. L’outil Krakatoa [MPMU04] suit ce principe, et permet de traduire automatiquement un programme Java en un programme Why avec une telle modélisation. L’outil Caduceus, en cours de développement, fait de même avec les programmes C.
Remarquons aussi que cette approche pour modéliser les structures de données complexes peut être aussi utilisée pour traiter les entiers bornés : il suffit d’interpréter les opérations arithmétiques comme l’addition par une autre fonction logique. On a même le choix de permettre les débordements et faire des calculs modulo 232, ou bien imposer le non-débordement, en introduisant une fonction d’addition sur les entiers non bornés mais avec précondition de la forme
parameter bounded_add : x:int -> y:int ->
{ -2^31 <= x+y < 2^31 } int { result = x+y }


