Next: Multi-tape S-attributed grammars
Up: A multi-tape S-attributed grammar's
Previous: A multi-tape S-attributed grammar's
We recall the basic definitions of context-free grammars and of their
natural extension to S-attributed grammars.
These definitions are adapted to the fact that we use this formalism
to model biological properties of sequences.
Definition 1
(
Context-free grammar)
A context-free grammar
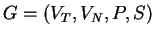
consists of a finite set of
terminals
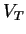
, a finite set of nonterminals
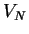
such that
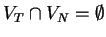
, a finite set of productions (rewriting rules)
P and a start symbol
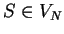
. Let
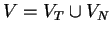
denote
the vocabulary for the grammar. Each production in
P has the
form
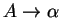
, where
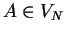
and
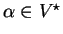
. A is the left-hand side of the production and
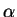
its
right-hand side.
The transitive closure of the derivation relation
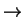 is
denoted
is
denoted
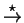 . A derivation tree is the
planar representation of a sequence of derivations
. A derivation tree is the
planar representation of a sequence of derivations
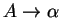 such that
such that 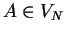 and
and
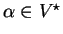 . The set of
strings in
. The set of
strings in
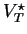 derived from S is called the language
generated by G and it is denoted by
derived from S is called the language
generated by G and it is denoted by 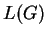 . The empty string is
denoted by
. The empty string is
denoted by
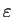 .
.
In order to keep the number of derivation
trees finite for a given word
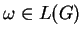 , we assume that
the grammar is non-circular, which means that no nonterminal
, we assume that
the grammar is non-circular, which means that no nonterminal 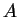 may
verify
may
verify
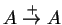 . We also assume that the
grammar is epsilon-free (i.e. it has no rules of the form
. We also assume that the
grammar is epsilon-free (i.e. it has no rules of the form
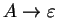 ). An ambiguous grammar is a grammar for which
there exists a string of symbols having at least two different
derivation trees. For example, the grammar whose derivation trees describe
t-RNA secondary structures has to be ambiguous because a given RNA has
potentially several different secondary structures. Parsing is the
process of finding a derivation tree for a string in
). An ambiguous grammar is a grammar for which
there exists a string of symbols having at least two different
derivation trees. For example, the grammar whose derivation trees describe
t-RNA secondary structures has to be ambiguous because a given RNA has
potentially several different secondary structures. Parsing is the
process of finding a derivation tree for a string in 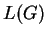 ,
which is called the parse tree of the sequence.
,
which is called the parse tree of the sequence.
S-attributed context-free grammars, which are a proper subset of
attributed-grammars introduced by Knuth in his seminal paper
[2], are an extension of context-free grammar allowing the
assignment of a value (called attribute) to every vertex of a
derivation tree.
Definition 2
(
S-attributed grammar)
An S-attributed grammar, denoted by
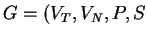
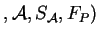
, is an extension of the context-free grammar
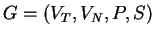
; an attribute
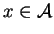
is attached
to each symbol
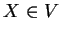
, and a string of attributes
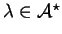
to each string
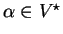
.
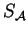
is a function from
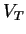
to
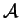
assigning attributes to
terminals.
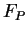
is a set of functions from
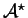
to
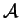
. A function
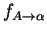
is in
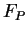
for
every production
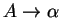
in P.
The attribute of a string
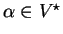 , denoted by
, denoted by
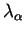 , is the concatenation of the attributes of the symbols in
, is the concatenation of the attributes of the symbols in
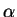 . When a function
. When a function
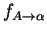 is applied to the
attribute
is applied to the
attribute
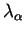 derived from A it returns the attribute
derived from A it returns the attribute
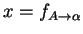 of
of 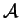 . Thus, the functions of
. Thus, the functions of 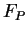 determine the bottom-up computation of the attributes of nonterminals A
in derivations
determine the bottom-up computation of the attributes of nonterminals A
in derivations
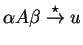 , where
u must belong to
, where
u must belong to 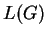 so that the attribute
of A be computable.
so that the attribute
of A be computable.
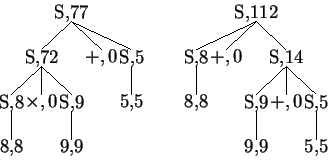
Example 1
We consider the following ambiguous context-free grammar for
arithmetical expressions.
We extend it into an S-attributed grammar such that each
attribute stores the value of the arithmetical expression corresponding to
the derivation subtree rooted at this node.
Thus, the sequence
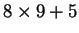 can be parsed in different
ways corresponding to different derivation trees, hence producing
different values
can be parsed in different
ways corresponding to different derivation trees, hence producing
different values
As previously noted, grammars used for biological sequence analysis
are ambiguous because
they aim at describing the space of all possible
configurations. Attributes are designed to give an
evaluation of the quality for each of them which gives a choice
criterion. For example, if the
attribute of a vertex is an energy or a probability, the criterion may
be the selection of the derivation tree with the lowest energy or the
highest probability at the root. (But attributes are not restricted to
simple real values in general even if this paper deals mainly with
this kind). The selection of the best possible value for an attribute
is done by means of a function called optimization constraint.
Definition 3
(
Optimization constraint)
Let G be an S-attributed grammar and let
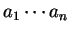
be a string of
L(G). Let x be the attribute of a derivation
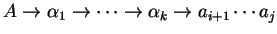
and let
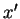
be the attribute of another derivation
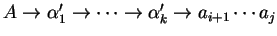
. The optimisation
constraint
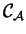
associated with the nonterminal A takes
as an input the attributes x and
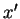
and returns another attribute
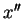
. We note
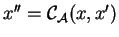
.
In practice,
 will be a comparison function
between
will be a comparison function
between 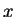 and
and
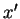 which returns the optimal attribute
(the lowest energy, if attributes are free energy). Finally, we
denote by
which returns the optimal attribute
(the lowest energy, if attributes are free energy). Finally, we
denote by
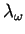 the optimal attribute of a string
the optimal attribute of a string
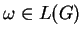 .
.



Next: Multi-tape S-attributed grammars
Up: A multi-tape S-attributed grammar's
Previous: A multi-tape S-attributed grammar's
Jerome Waldispuhl
2002-12-18
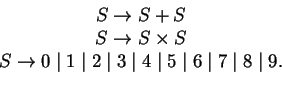
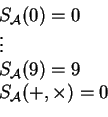
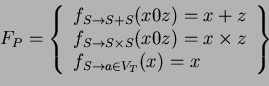
![]() can be parsed in different
ways corresponding to different derivation trees, hence producing
different values
can be parsed in different
ways corresponding to different derivation trees, hence producing
different values