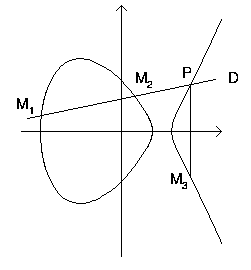

Une courbe elliptique est définie par une équation du type y2 + (a1 x + a3) y = x3 + a2 x2 + a4 x+ a6 ; on peut la munir d'une loi de groupe comme indiquée sur la figure ci-dessus, où M3 est la somme de M1 et M2. L'utilisation des courbes elliptiques en théorie algorithmique des nombres remonte à 1987, date à laquelle Lenstra a mis au point une méthode de factorisation utilisant ces objets [Lenstra87]. De nombreuses autres applications ont suivi: primalité d'entiers [GoKi86], [AtMo93b]; systèmes cryptographiques (voir par exemple [Menezes93], [Enge99]).
Pour en savoir plus:| Taille en chiffres décimaux | Qui | Quand |
| 65 | Atkin | 24/02/1991 |
| 75 | Atkin | 14/02/1992 |
| 100 | Atkin | 24/02/1992 |
| 120 | Atkin | 24/07/1992 |
| 130 | Atkin | 24/07/1992 |
| 150 | Atkin | 29/03/1992 |
| 200 | Atkin | 24/07/1992 |
| 225 | Atkin | ??/07/1993 |
| 250 | FM | 07/02/1994 |
| 276 | Atkin | 29/03/1994 |
| 350 | RL-FM | ??/04/1994 |
| 376 | Müller | ??/04/1994 |
| 400 | RL-FM | 03/10/1994 |
| 425 | Müller | ??/10/1994 |
| 500 | RL-FM | 27/01/1995 |
En 1999, Satoh a introduit les méthodes p-adiques dans le calcul de la cardinalité en se servant du relèvement canonique d'une courbe elliptique. Dans un corps de pn éléments pour un p fixé, son algorithme déterministe a une complexité de O (n3 + epsilon). Le coup d'envoi de la mise en pratique de cet algorithme a été donné par Fouquet, Gaudry et Harley qui ont proposé une extension au cas de p=2. Ce cas n'était pas traité dans l'article de Satoh bien qu'ayant le plus d'intérêt pratique (cette extension a été effectuée indépendamment par Skjernaa). Des expériences pratiques ont permis d'une part de pulvériser les précédents records (passant de 2000 à 8000 bits) et d'autre part de gagner un ordre de grandeur sur les temps de calcul pour les tailles utiles en cryptographie.
Des améliorations se sont succédées et les différentes alternatives sur le marché actuellement incluent l'algorithme de Vercauteren et al. qui réduit la complexité spatiale à O (n2), la méthode AGM inventée par Mestre et développée par Gaudry et Harley qui présente les mêmes avantages tout en améliorant les constantes, et dernièrement la méthode de Satoh-Skjernaa-Taguchi (SST) qui améliore la complexité théorique au prix de quelques précalculs. De nouveaux progrès sont encore en cours ou à venir (voir le récent record de Harley à 32000 bits).
| taille | Qui | Quand | Méthode |
| 300 | RL-FM | ??/09/94 | SEA |
| 400 | RL-FM | 28/09/94 | SEA |
| 500 | RL-FM | 18/10/94 | SEA |
| 601 | RL-FM | 27/12/94 | SEA |
| 701 | RL-FM | 10/03/95 | SEA |
| 1009 | RL-FM | 31/07/95 | SEA |
| 1301 | RL-FM | ??/04/96 | SEA |
| 1663 | RL-Joux | 19/06/98 | SEA |
| 1999 | Vercauteren | 17/10/99 | SEA |
| 3001 | Fouquet-Gaudry-Harley | 10/05/2000 | Satoh-FGH |
| 8009 | Fouquet-Gaudry-Harley | 05/10/2000 | Satoh-FGH |
| 16001 | Harley | ??/??/2001 | AGM |
| 32003 | Harley | 20/08/02 | p-adique |
La théorie de la multiplication complexe fournit une alternative aux algorithmes de calcul du cardinal, car elle permet de construire sur mesure des courbes dont le cardinal est connu d'avance. Les algorithmes qui en ressortent sont au cœur des preuves de primalité d'ECPP. Il servent également à la construction de cryptosystèmes elliptiques. Notre équipe a fait de nombreuses contributions dans ce domaine.
Pour en savoir plus: