La première apparition d'une notion apparentée aux systèmes plats a
été retrouvée dans un article de David Hilbert en 1912, sous le nom de
«integralloss system», c'est-à-dire de système dont les solutions
peuvent être exprimées sans intégration. En 1915, Élie Cartan en a
donné la caractérisation suivante dans un cas particulier, qui
correspond pour l'automatique contemporaine à celui de systèmes à deux
commandes sans dérives, c'est-à-dire de la forme:
THÉORÈME 19. -- Considérons un système sans dérive. On définit les espaces vectoriels
![]() comme suit :
comme suit :
![]() ,
...
,
...
![]() .
Un système à deux commande sans dérive est plat ssi pour tout
.
Un système à deux commande sans dérive est plat ssi pour tout ![]() , l'espace vectoriel
, l'espace vectoriel ![]() est de dimension
est de dimension ![]() Cette condition est trivialement satisfaite pour
Cette condition est trivialement satisfaite pour ![]() . Le cas
. Le cas
![]() correspond à l'exemple de la voiture,
correspond à l'exemple de la voiture, ![]() à celui d'un camion
avec remorque.
à celui d'un camion
avec remorque.
THÉORÈME 20. -- Un système sans dérive
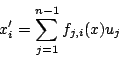
Nous ne détaillons pas la preuve, nous contentant décrire comment
on peut obtenir des sorties linéarisantes. Posons
![]() . Soient
. Soient
![]() , ...,
, ..., ![]() ,
, ![]() fonctions de l'état. On
considère la dérivation
fonctions de l'état. On
considère la dérivation
![]() . On prend pour
. On prend pour ![]() , ...,
, ...,
![]() ,
, ![]() solution fonctionnellement indépendantes de
l'équation aux dérivées partielles linéaire
solution fonctionnellement indépendantes de
l'équation aux dérivées partielles linéaire
![]() . Celles-ci forment alors (pour un choix «
générique» des
. Celles-ci forment alors (pour un choix «
générique» des ![]() ) une sortie linéarisante, car
) une sortie linéarisante, car
![]() , ce qui montre que
la matrice jacobienne
, ce qui montre que
la matrice jacobienne
![]() n'est pas de
rang maximal
n'est pas de
rang maximal ![]() , ce qui permet d'exprimer localement l'état
, ce qui permet d'exprimer localement l'état
![]() , connaissant
, connaissant ![]() et
et ![]() , si
, si
Exemple 21. -- La voiture est un bon exemple. Si l'on prend
![]() , on obtient aisément comme solution
, on obtient aisément comme solution ![]() et
et
![]() . Ce type de solution présente l'inconvénient
de n'être pas invariante par le groupe des translations et des
rotations. Or, on souhaite un contrôle qui ne dépende pas du choix des
coordonnées.
. Ce type de solution présente l'inconvénient
de n'être pas invariante par le groupe des translations et des
rotations. Or, on souhaite un contrôle qui ne dépende pas du choix des
coordonnées.
Pour cela, il faut prendre un champs ![]() dont l'expression soit
invariante par le groupe:
dont l'expression soit
invariante par le groupe:
![]() . Pour
. Pour ![]() , on
obtient des sorties linéarisantes qui correspondent aux
coordonnées d'un point de l'essieu arrière (l'intersection de
la droite d'angle
, on
obtient des sorties linéarisantes qui correspondent aux
coordonnées d'un point de l'essieu arrière (l'intersection de
la droite d'angle ![]() dans le référentiel du
véhicule passant par le point de référence choisi sur
celui-ci. Quand
dans le référentiel du
véhicule passant par le point de référence choisi sur
celui-ci. Quand ![]() tend vers
tend vers ![]() , ce point d'intersection tend
vers l'infini. On obtient alors des sorties linéarisantes
, ce point d'intersection tend
vers l'infini. On obtient alors des sorties linéarisantes
![]() et
et
![]() . Celles-ci ne
sont plus préservées que par les rotations par rapport à
l'origine.
. Celles-ci ne
sont plus préservées que par les rotations par rapport à
l'origine.
Détailler les calculs est un excellent exercice.